Toroidal inductors are often used in pulsed power and power conditioning applications since the magnetic fields are largely confined within the volume of the form. All of the formulas on this page are shown assuming an air core toroidal inductor. If one uses a magnetic core as a form to wind the toroid on, the inductance of the toroid can be found by calculating the value from the appropriate formula shown below for the air core inductor and then multiplying that value by the relative permeability of the magnetic core material.

Toroids may be wound on a circular form as shown in the figure below:

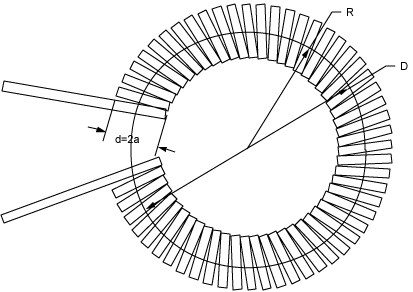
The inductance for such a toroid can be calculated from the equation below:

where N is the number of turns, R is the mean radius of the form as shown in the figure (in cm), and a is the radius of the windings on the form as shown in the figure (in cm).

Another formula for the inductance of a circular cross section toroid is shown below:

where N is the number of turns, D is the mean diameter of the form as shown in the figure (in inches), and d is the diameter of the windings as shown in the figure (in inches).

They may also be wound on a rectangular form as shown in the figure below:

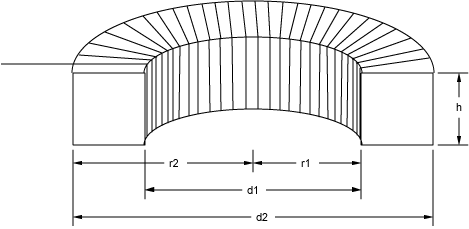
The inductance for a rectangular cross section toroid can be found from the following equation (Terman, Frederick E., Radio Engineers Handbook, McGraw-Hill, New York, 1943, p58.):

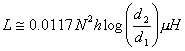
where N is the number of turns, h is the height of the winding (in inches), d₁ is the inner diameter (in inches), and d₂ is the outer diameter (in inches).

A second formula for a rectangular form toroid is shown below:

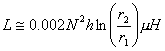
where N is the number of turns, h is the height of the winding (in cm), r₁ is the inner radius (in cm), and r₂ is the outer radius (in cm).

The calculator below can be used to determine the proper internal resistor values for an attenuator of a given configuration (based on attenuation factor and matching impedance). It will also determine the attenuation in dB. Credit for the initial Javascript code used in the calculator is given to Ray Allen who has a number of similar useful calculators on his website, Pulsed Power Portal.